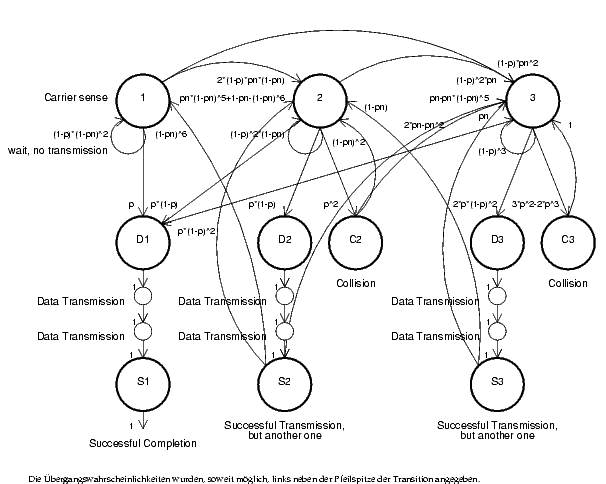
Entwicklung des Markov-Modells
Um die Übersicht zu gewährleisten, wurde das Markov-Modell beispielhaft für 3 Stationen entwickelt. Eine Erweiterung auf mehrere Stationen ist zwar konzeptuell nicht schwierig, kann aber durch die vielen auftretenden Zustandsübergänge und komplexen Wahrscheinlichkeiten unübersichtlich werden.
Im folgenden wird die Wahrscheinlichkeit, dass sich eine Station in einem Zeitslot entscheidet zu senden, mit "p" bezeichnet. Die Wahrscheinlichkeit, dass eine Station, die noch keinen Sendebedarf hat, einen Sendebedarf in einem Zeitslot bekommt, wird mit "pn" bezeichnet.
Stationen, die während der Betrachtung erst Sendebedarf bekommen, werden im Modell erst dann berücksichtigt, wenn der Kanal frei ist. Bei belegtem Kanal, müssen diese Stationen sowieso warten, bis der Kanal frei wird und können dadurch den Ablauf noch nicht beeinflussen.
Zustand "1"
Nur die betrachtete Station hat einen Sendebedarf. Mit der Wahrscheinlichkeit "p" beginnt die betrachtete Station mit dem Senden der Daten und geht in den Zustand "D1" über. Da nun der Kanal belegt ist, kann keine andere Station die Datenübertragung mehr stören, so dass die Datenübertragung nach "d" Slots erfolgreich abgeschlossen werden kann.
Mit der Wahrscheinlichkeit "1-p" entscheidet die betrachtete Station, in diesem Slot nicht zu senden. Abhängig davon, wie viele Stationen nun einen Sendebedarf bekommen, erfolgt der Zustandsübergang nach "1", "2" oder "3" mit den entsprechenden Wahrscheinlichkeiten, die sich auf "1-p" addieren.
Wahrscheinlichkeit "1" -> "1"
Mit Wahrscheinlichkeit "1-p" sendet die betrachtete Station nicht und jeweils mit Wahrscheinlichkeit "1-pn" bekommen die zwei restlichen Stationen keinen Sendebedarf.
Anmerkung: P(1, 1) = (1-p)*(1-pn)^2
Wahrscheinlichkeit "1" -> "2"
Eine der beiden inaktiven Stationen bekommt Sendebedarf. (Voraussetzung: die betrachtete Station sendet mit Wahrscheinlichkeit "1-p" nicht)
Anmerkung: P(1, 2) = (1-p)*2*pn*(1-pn)
Wahrscheinlichkeit "1" -> "3"
Beide zuvor inaktiven Stationen bekommen Sendbedarf. (Voraussetzung: die betrachtete Station sendet mit Wahrscheinlichkeit "1-p" nicht)
Anmerkung: P(1, 3) = (1-p)*pn^2
Zustand "2"
Die betrachtete Station und eine beliebige weitere Station haben Sendebedarf. Entscheidet nun die betrachtete Station zu senden und die zweite Station nicht zu senden (Wahrscheinlichkeit "p*(1-p)"), erfolgt ein Übergang nach "D1". Mit gleicher Wahrscheinlichkeit kann auch der Fall eintreten, dass die betrachtete Station nicht sendet, aber die zweite Station sendet, worauf ein Zustandsübergang nach "D2" erfolgt. Entscheiden sich beide Stationen zu senden, tritt eine Kollision auf, die durch einen Zustandsübergang nach "C2" im Markov-Modell abgebildet ist. Wie im Zustand "1" kann auch der Fall eintreten, dass keiner sendet, was sich in Zustandsübergänge nach "2" bzw. "3" auswirkt - abhängig, ob in der Zwischenzeit nun auch die dritte Station einen Sendebedarf hat oder nicht.
Wahrscheinlichkeit "2" -> "D1"
Die betrachtete Station entscheidet mit "p" zu senden, die zweite Station entscheidet mit "1-p", nicht zu senden.
Anmerkung: P(2, D1) = p*(1-p)
Wahrscheinlichkeit "2" -> "D2"
Die betrachtete Station entscheidet mit "1-p", nicht zu senden, die zweite Station entscheidet mit "p" zu senden.
Anmerkung: P(2, D1) = (1-p)*p
Wahrscheinlichkeit "2" -> "C2"
Beide Stationen entscheiden sich jeweils mit Wahrscheinlichkeit "p" zu senden.
Anmerkung: P(2, C2) = p^2
Wahrscheinlichkeit "2" -> "2"
Beide Stationen entscheiden sich jeweils mit Wahrscheinlichkeit "1-p", nicht zu senden, und mit Wahrscheinlichkeit "1-pn" bekommt die dritte Station auch keinen Sendebedarf.
Anmerkung: P(2, 2) = (1-p)^2*(1-pn)
Wahrscheinlichkeit "2" -> "3"
Beide Stationen entscheiden sich jeweils mit Wahrscheinlichkeit "1-p", nicht zu senden, und mit Wahrscheinlichkeit "pn" bekommt die dritte Station Sendebedarf.
Anmerkung: P(2, 3) = (1-p)^2*pn
Zustand "3"
Hier haben alle drei Stationen einen Sendebedarf. Wie im Zustand "2" kann entweder die betrachtete Station als einzige senden, es kann eine andere Station als einzige senden, es kann eine Kollision auftreten oder es kann mit Wahrscheinlichkeit "(1-p)^3" keiner senden.
Kollision: Zustände "C2", "C3"
Tritt eine Kollision auf, wird in den Zustand, der der Anzahl der Stationen mit Sendebedarf entspricht, zurückverzweigt.
Wahrscheinlichkeit "C2" -> "2"
Mit Wahrscheinlichkeit "1-pn" bekommt die dritte Station je Zeitslot keinen Sendebedarf.
Anmerkung: P(C2, 2) = (1-pn)^2
Wahrscheinlichkeit "C2" -> "3"
Anmerkung: P(C2, 3) = 1 - (1-pn)^2 = 2*pn - pn^2
Erfolgreiches Senden der betrachteten Station: Zustand "S1"
Der gewünschte Endzustand ist erreicht.
Erfolgreiches Senden einer anderen Station: Zustände "S2", "S3"
Nach dem erfolgreichen Senden wird in den Zustand, der der Anzahl der Stationen, die noch Sendebedarf haben, entspricht, zurückverzweigt.
Wahrscheinlichkeit "S2" -> "1"
Mit Wahrscheinlichkeit "1-pn" bekommt die dritte Station je Zeitslot (1 Slot Carrier Sensing, 4 Slots für die Datenübertragung) keinen Sendebedarf. Nach dem Senden bekommt auch die Station, die gerade gesendet hat, nicht gleich wieder Sendebedarf.
Anmerkung: P(S2, 1) = (1-pn)^5*(1-pn) = (1-pn)^6
Wahrscheinlichkeit "S2" -> "2"
Die dritte Station kann während der Datenübertragung Sendebedarf bekommen (Wahrscheinlichkeit "1-(1-pn)^5") und die übertragende Station nachher nicht gleich wieder sofort (Wahrscheinlichkeit "1-pn"). Oder es kann die übertragende Station gleich wieder Sendebedarf bekommen (Wahrscheinlichkeit "pn"), aber die dritte Station nicht (Wahrscheinlichkeit "(1-pn)^6").
Anmerkung: P(S2, 2) = (1-(1-pn)^5)*(1-pn) + pn*(1-pn)^5 = pn*(1-pn)^5 + 1 - pn - (1-pn)^6
Wahrscheinlichkeit "S2" -> "3"
Beide Stationen bekommen während der Datenübertragung Sendebedarf.
Anmerkung: P(S2, 3) = pn*(1-(1-pn)^5) = pn - pn*(1-pn)^5